The Rules for Converting Apparent to Mean Time and Vice Versa

The difference between LAT reckoning and LMT reckoning is called the equation of time. The value of the equation of time must be found in order to convert apparent time to its mean time equivalent. In the example of Marie-Antoinette given earlier, the equation of time is 16 minutes and 12 seconds. For the current era, since the equation of time changes slowly over a period of decades, one could simply go to a table with the values of the equation of time throughout the course of the year and take out an approximation that would not be far wrong; but because the equation of time changes substantially over centuries as the date of perihelion and other orbital factors change, recourse to a modern table will not do for an earlier period.

The equation of time can be seen in several equivalent forms, first as the difference between apparent and mean time; second, as the difference between the hour angle of the true Sun and the hour angle of the mean Sun; and also, as the difference between the right ascension of the apparent Sun (RAAS) and the right ascension of the mean Sun (RAMS).

Most computer programs will generate right ascension (RA) and declination coordinates. RA should be in time, not arc. If your program gives RA only in arc, divide the value it gives you for any particular time by 15 because the Earth rotates 15° in one hour. For example, 350° 17′ 29″ / 15 = 23h 21m 10s. If your program cannot produce RA, it can be derived in the following way:

The RAAS can be calculated from this modest equation:

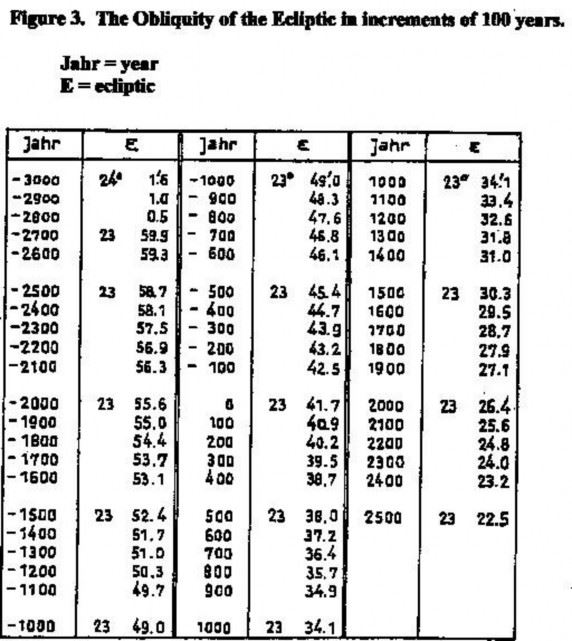
Since the obliquity of the ecliptic varies by more than two degrees over several tens of millennia, the values for the last several thousand years at one hundred-year intervals are included in figure 3 below.

The RAMS is the same as the RA of the MC (or local sidereal time) at local mean time noon (not zone time noon). Then multiply the difference between the previous local mean time noon and the birthtime by 9.856 seconds per hour and add those seconds to the RAMS at noon.

____________________
Table 1.

Determine the values of the right ascension of the apparent Sun (RAAS) and the right ascension of the mean Sun (RAMS) for the birth data.

If the RAMS is greater than the RAAS, the equation of time (E of T) is positive (+). If the RAAS is greater than the RAMS, the equation of time (E of T) is negative (-).

Then, having arrived at the value of the E of T, apply it to one of the following four rules:

1. If the birthtime was reckoned in apparent time and the E of T is +, SUBTRACT the E of T from the apparent time to get the mean time equivalent.
2. If the birthtime was reckoned in apparent time and the E of T is -, ADD the E of T to the apparent time to get the mean time equivalent.
3. If the birthtime was reckoned in mean time and the E of T is +, ADD the E of T to the mean time to get the apparent time equivalent.
4. If the birthtime was reckoned in mean time and the E of T is -, SUBTRACT the E of T from the mean time to get the apparent time equivalent.

____________________

The following worked example illustrates how accurately a horoscope could be set up more than four hundred years ago, if attention is paid to the time standard in place then, instead of applying LMT to every old horoscope no matter what its date.

The discovery of a horoscope at the University of California at Santa Cruz attributed to the hand of Johannes Kepler (1571-1629) is typical of the horoscopes of the day.

It is cast in terms of the tropical zodiac for 5:00 p.m. local apparent time on September 10, 1586 in the Old Style, that is, Julian calendar reckoning (the Gregorian or New Style dates from October 15, 1582 but not all countries and regions in Europe adopted it immediately).

Because Kepler gave no minutes for the angles or the lights, the horoscope could be set up for a fairly wide swath of longitude between approximately Munich, Germany to Vienna, Austria which are both on 48° North. The house system used was Regiomontanus, the standard of the day. For 5:00 p.m. (LMT since we don’t know yet what the LMT equivalent is that corresponds to 5:00 p.m. LAT), September 10, 1586 in the Old Style (Julian calendar), the following values obtain:

11h 56m 35s = RAMS
– 11h 49m 50s = RAAS
6m 45s = E of T

As the RAMS is greater than the RAAS, the equation of time is positive. Since the time in the document is rendered in terms of apparent time and the equation of time is positive, we subtract the equation of time from the apparent time to get the mean time equivalent; and since the E of T will not change over the course of six minutes of mean solar time, the same value applies to both the E of T at 5:00 p.m. LAT and 5:00 p.m. LMT.

5:00:00 p.m. LAT
– 0:06:45 E of T    
4:53:15

+ 0:00:01  mean time-sidereal time interval
4:53:16 p.m. LMT

The equation of time at 5:00 p.m. LMT was +6minutes 45seconds, but this value of the E of T is in terms of right ascension, which is reckoned in mean sidereal time.

To go from sidereal to mean time requires that the acceleration be subtracted, but we can account for the difference between sidereal time and mean time by adding 1 second to 4:53:15 for the acceleration on 6m 45s.

• The result gives the value of the equation of time in terms of mean solar time: 6m 44s.
• The angles and positions of the planets answer to 4:53:16 PM LMT, and are a best fit for Munich (48° N 08′ and 11° E 35′).

The use of apparent time is particularly helpful in rectifying charts when the equation of time is large. For example, George Washington’s birth was written in the family bible as having occurred “about 10 in the morning” of February 11, 1731/32. England and the American colonies used the Annunciation Style in those days according to which the year turned not on January 1 but on March 25. (The Annunciation Style refers to the announcement by the angel Gabriel to Mary that she was carrying the Christ child, as described in Luke 1:28-35. The date of the Annunciation is March 25, which Christian churches still commemorate as the day of the announcement of the Incarnation.)

So it was still 1731 according to the Annunciation Style in February of what we now call 1732. In addition, Washington’s birth was recorded in the Julian Style of calendar reckoning (England and the American colonies did not adopt the Gregorian calendar until 1752).

The Gregorian equivalent is February 22, 1732.

At ten in the morning on that day near what is now Wakefield, Virginia, where Washington was born, the equation of time was -14 minutes and 1 second; so before the first test has been applied to that time, a base chart of 10:14:01 a.m. LMT has to be set up (see figure 4) to avoid the fundamental error of assuming that LMT was the time standard during an era when it didn’t exist.

The best angular fits in his solar and lunar returns and his neo-solar quotidian progressions for his marriage, victory at Yorktown, swearing in as first president and his death suggest a birthtime of 9:58 a.m. LAT (10:12:01 a.m. LMT) which is certainly still “about 10 in the morning.”

Note that Marie-Antoinette’s equation of time was +16 minutes and 12 seconds, so in her case the equation of time had to be subtracted from the LAT value. The best fits for her marriage, ascension to the throne, births of her children and death by guillotine, respond to 7:29 p.m. LAT (7:12:48 p.m. LMT). Rectification is easier if the right base time is used.

Finally, to reiterate, all birthtimes until late in the eighteenth century at the earliest, are in terms of local apparent time.

The tendency to ignore local apparent time should be seen for what it is: a gross oversight, which can be easily remedied by recourse to the determination of the equation of time for horoscopes, which pre-date the modern period.

*******************

The following table of the Equation of Time shows the difference between mean time and apparent time in 1999 at ten-day intervals. Minutes and seconds preceded by + means that the Sun is fast of the clock by the amount shown in the table; i.e. the Sun comes to the M.C. before local mean time noon, so that at mean time noon, the Sun will be in the 9th house. Minutes and seconds preceded by – means that the Sun is slow of the clock by the amount shown in the table; i.e. at mean time noon the Sun will not have reached the M.C. and will appear in the 10th house. The low precision maximum values are – 14m 13s on February 12 and +16m 26s on November 3. The Equation of Time is zero in 1999 on April 16, June 12, September 1 and December 25.

This article was previously published in 2000 in The Mountain Astrologer.

______________
Works Consulted

1. Ahnert, Paul. Astronomische-chronologische Tafeln für Sonne, Mond und Planeten. Leipzig: Johann Ambrosius Barth Verlag, 1960.
2. Andrewes, William J. H. “Time for the Astronomer.” Vistas in Astronomy 28 (1995).
3. The Astronomical Almanac for the Year 1999. Washington D.C.: U.S. Government Printing Office, 1998.
4. Barbault, André. Traité Pratique D’Astrologie. Paris: Éditions du Seuil, 1961.
5. Bartky, Ian R. “Inventing, Introducing and Objecting to Standard Time.” Vistas in Astronomy 28 (1985).
6. Chapman, Allan. “Christiaan Huygens (1629-95): astronomer and mechanician.” Endeavour n.s. 19 (1995).
7. Chauvenet, William. Spherical and Practical Astronomy. 5th ed. Philadelphia: J. B. Lippincott, 1887.
8. Congressional Globe. Twenty-Ninth Congress, First Session, December 1, 1845-August 10,1846. Washington D.C.: Blair & Rives, 1846.
9. Covey, Curt. “The Earth’s Orbit and the Ice Ages.” Scientific American, February 1984, 250. Daumas, Maurice. “Le faux échappement de Villard de Honnecourt.” Revue D’Histoire Des Sciences 35 (1982).
10. Dohrn-van Rossum, Gerhard. History of the Hour. Chicago: University of Chicago Press, 1996.
11. Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. London: Her Majesty’s Stationery Office, 1961; reprint, London: Her Majesty’s Stationery Office, 1974; 4th impression, 1977.
12. Fraser, J. T., ed. The Voices of Time. 2nd ed. Amherst: University of Massachusetts Press, 1981.
13. Freeman, Douglas Southall. George Washington. vol. 1. New York: Charles Scribner’s Sons.
14. Guye, Samuel and Henri Michel. Time and Space. New York: Praeger Press, 1971. 1948.
15. Howse, Derek. Greenwich Time. Oxford: Oxford University Press, 1980.
16. Hutchinson, Beresford. “Guardians of Greenwich Time.” Vistas in Astronomy 28 (1985).
17. Jaquet, Eugène and Alfred Chapuis. The Technique and History of the Swiss Watch. London, Spring Press, 1970.
18. Kibre, Pearl. Studies in Medieval Science, Alchemy, Astrology, Mathematics and Medecine. London: Hambledon Press, 1984.
19. Landes, David S. Revolution in Time. Cambridge: Belknap Press of Harvard University Press, 1983.
20. Mayr, Otto. Authority, Liberty and Automatic Machinery in Early Modern Europe. Baltimore: Johns Hopkins University Press, 1986.
21. Meeus, Jean. Mathematical Astronomy Morsels. Richmond: Willman-Bell, 1997.
22. Merzbach, Uta C. “Calendars and Reckoning of Time.” Dictionary of the Middle Ages, vol. 3. New York: Charles Scribner’s Sons, 1983.
23. Mueller, Ivan I. Spherical and Practical Astronomy. New York: Frederick Ungar, 1969; reprint, New York: Frederick Ungar, 1977.
24. Quinlan-McGrath, Mary. “The Villa Farnesina, Time-Telling Conventions and Renaissance Astrological Practice.” Journal of the Warburg and Courtauld Institutes 58 (1995).
25. Quinones, Ricardo J. The Renaissance Discovery of Time. Cambridge: Harvard University Press, 1972.
26. Sherman, Stuart. Telling Time. Chicago: University of Chicago Press, 1996.
27. Thompson, E. P. Customs in Common. New York: New Press, 1991.
28. Turner, A.J. Of Time and Measurement. Aldershot: Variorum, 1993.