What is the Astronomical Rationale of LAT?

Local apparent time is a variable rate because the Sun’s apparent daily motion is variable, and this for two reasons:

• first, the obliquity of the ecliptic, and
• second, the ellipticity of the Earth’s orbit.

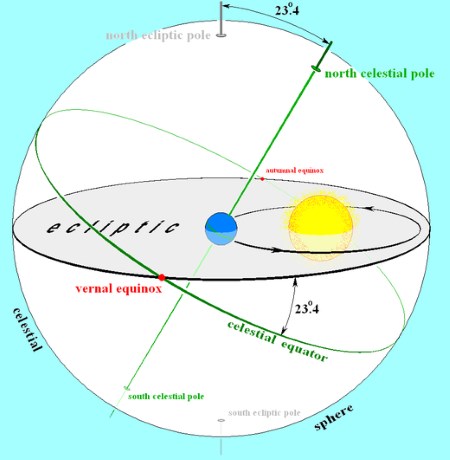The ecliptic is the plane of the Earth’s revolution about the Sun. The celestial equator, which is the Earth’s equator extended out into space, is the plane of the Earth’s rotation. The angle between these two planes, currently 23° 26′ 16″, is the obliquity of the ecliptic.

As the planes of rotation and revolution are not the same, it follows that since the Sun moves in the ecliptic, equal changes in celestial longitude, which is reckoned along the ecliptic will not produce equal changes in right ascension which is reckoned along the equator. Additionally, the Earth’s orbit is an ellipse, not a circle, which requires that the Earth move faster at perihelion, slower at aphelion and at other speeds between these two extremes.

Seen in another way, if the Earth’s spin axis was not inclined to the plane of its orbit but straight up, perpendicular to the ecliptic, and the Earth’s orbit was a circle instead of an ellipse, there would no seasons and no such condition as apparent time, only one unvarying climate state and one unvarying time state.

The consequence then of the Earth’s elliptical orbit and the obliquity of the celestial equator to the ecliptic is that the Sun’s daily motion is variable. A clock set to a mean time standard, because such a standard is not synchronized to the Sun, demonstrates that variability, but until the going of any clock was accurate enough to demonstrate it, there was no reason to think about invoking a mean time standard, even though use of a such a standard facilitates astronomical computations. The central issue is that there was no more reliable standard with less variation than the Sun until clocks became consistently less variable than the Sun.

The first major by-product of accurate clocks that ultimately benefited astrologers was the determination of sidereal time in 1678 by John Flamsteed, the first Astronomer Royale at the Greenwich Observatory, which had been established in 1675. The clocks Flamsteed commissioned for the observatory were the most accurate in the world at the time, and the first to be set to Greenwich Mean Time; also the adoption of the local mean time of the Greenwich Observatory in 1676 is probably the first official application of a mean time standard anywhere. It remained, however, an astronomical, not a civil standard, until 1792.

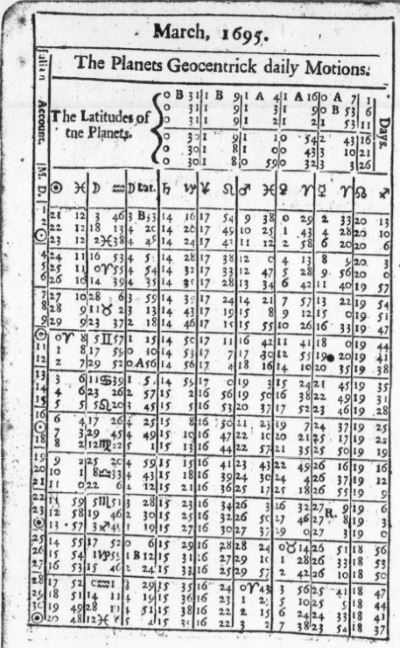
Ephemerides for the sixteenth, seventeenth and generally the eighteenth centuries did not have a tabular entry for sidereal time (see figure 2 on the left, a typical 17th century English ephemeris) because until Flamsteed determined the rate, it was not known that the Earth’s daily rotation is uniform as there had not been clocks available heretofore that were accurate enough to demonstrate it.

Sidereal time is a measure of rotation.

The Earth rotates on its spin axis in 23 hours 56 minutes and 04.09054 seconds of mean solar time which equals 24:00:00 hours of mean sidereal time, a faster rate; therefore 24 hours of mean solar time takes 24 hours 03 minutes and 56.55535 seconds of mean sidereal time, so when you add the “acceleration on the interval” (9.856 seconds per hour) if you do your charts by hand, you’re taking into account the acceleration of mean sidereal time on mean solar time. Actually the Earth’s rate of rotation is not uniform due to tidal and atmospheric friction, the effect of the seasons and changes in the mantle and molten core; but the variation from an unvarying rate is so minuscule that Flamsteed’s 1678 value was good enough to last well into the nineteenth century for navigational and most other purposes.